Rapport technique sur l'échantillonnage et la pondération, Recensement de la population, 2021
7. Inférence statistique
L’inférence statistique dans le contexte de l’échantillonnage d’enquête est le processus visant à tirer des conclusions sur la population à partir des données recueillies auprès des répondants à l’enquête. Pour tirer des conclusions sur la population cible de l’enquête-échantillon du questionnaire détaillé à l’aide des estimations produites à partir de l’échantillon, l’incertitude associée à ces estimations doit être prise en considération. Comme décrit au chapitre 6, les estimations produites à partir de l’échantillon du questionnaire détaillé sont sujettes à la variabilité due à l’échantillonnage et à la non-réponse. La variance pour chaque estimation est une mesure qui permet de quantifier cette variabilité. Les estimations de la variance d’une statistique issue d’une enquête peuvent être utilisées pour produire d’autres mesures de la qualité des statistiques qui reflètent leur variabilité, mais qui sont plus faciles à interpréter que les estimations de la variance elles-mêmes. Ces mesures comprennent les erreurs-types, les coefficients de variation et les intervalles de confiance. Parmi ces mesures, les intervalles de confiance ont l’avantage de permettre aux utilisateurs de réaliser facilement des inférences statistiques. Pour cette raison, l’intervalle de confiance a été choisi comme indicateur de qualité fondé sur la variance pour accompagner les estimations du questionnaire détaillé du Recensement de 2021.
7.1 Intervalles de confiance et leur interprétation
Un intervalle de confiance associé à une estimation est un intervalle calculé autour de l’estimation pour refléter l’incertitude de l’estimation. Un intervalle de confiance est associé à un niveau de confiance, exprimé en pourcentage. Le niveau de confiance indique dans quelle mesure on peut être certain que le paramètre réel de population se trouve à l’intérieur de l’intervalle de confiance. Un niveau de confiance par défaut est généralement établi pour une enquête ou dans un domaine d’études en fonction des besoins des utilisateurs. Un niveau de confiance couramment utilisé est 95 %, et il s’agit du niveau de confiance par défaut pour le système de diffusion des données du recensement. Lorsqu’un utilisateur dispose d’un intervalle de confiance de 95 % pour une estimation, il peut dire qu’il est confiant à 95 % que le paramètre réel de population se trouve à l’intérieur de l’intervalle.
Une interprétation rigoureuse des intervalles de confiance repose sur des répétitions hypothétiques des méthodes d’échantillonnage et d’estimation. Cette interprétation est illustrée à la figure 7.1.1.
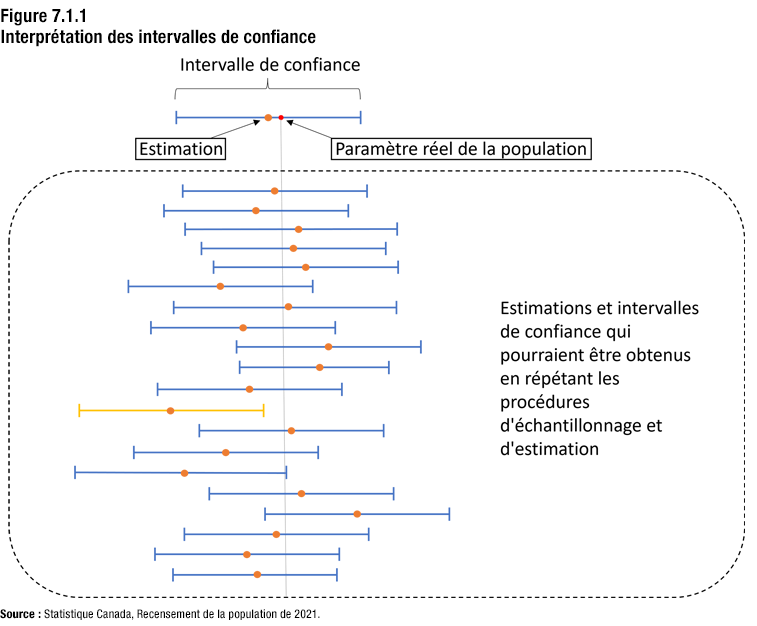
Description de la figure 7.1.1
En haut de la figure 7.1.1 se trouve une ligne horizontale représentant un intervalle de confiance. Un point orange se trouve près du milieu de la ligne. Il représente l’estimation du paramètre de population. Sur la ligne, à la droite du point orange, il y a un point rouge qui indique le paramètre réel de population.
Sous l’intervalle de confiance se trouve un large encadré qui contient 20 lignes horizontales semblables; elles représentent différents intervalles de confiance. La position horizontale de chacun de ces 20 intervalles de confiance est différente, et la longueur des intervalles de confiance varie aussi quelque peu. Près du centre de chacun des 20 intervalles de confiance, il y a un point orange qui indique l’estimation du paramètre de population. Ces 20 estimations et leurs intervalles de confiance correspondants représentent les estimations et les intervalles de confiance qui pourraient être obtenus en répétant hypothétiquement 20 fois les procédures d’échantillonnage et d’estimation.
Une ligne verticale descend dans le diagramme à partir du paramètre réel de population représenté dans l’intervalle de confiance au haut du diagramme. Cette ligne sert à indiquer si le paramètre réel de population est contenu dans chacun des 20 intervalles de confiance différents. Les intervalles de confiance qui croisent la ligne verticale contiennent le paramètre réel de population. Sur les 20 intervalles de confiance, 19 sont codés en bleu pour montrer qu’ils contiennent le paramètre réel de population, tandis que l’intervalle de confiance restant est codé en jaune pour montrer qu’il ne contient pas ce paramètre.
Source : Statistique Canada, Recensement de la population de 2021.
Description complète :
La partie supérieure de la figure 7.1.1 représente un intervalle de confiance associé à l’estimation d’un paramètre de population. Le paramètre réel de population se trouve à l’intérieur de cet intervalle de confiance.
La figure montre également les différentes estimations qui peuvent être produites en répétant hypothétiquement les procédures d’échantillonnage et d’estimation plusieurs fois avec leurs intervalles de confiance correspondants. Dans le cas du questionnaire détaillé, cet échantillonnage et cette estimation répétés seraient effectués en tirant un très grand nombre d’échantillons à partir de l’univers pour l’échantillon du questionnaire détaillé conformément au plan d’échantillonnage décrit au chapitre 2. Chacun des échantillons subirait les mêmes étapes de traitement, de pondération et d’estimation que l’échantillon réel. En général, les estimations et les intervalles de confiance produits pour une caractéristique donnée varieraient selon les échantillons. Cependant, si les hypothèses sous-jacentes de la méthode d’intervalle de confiance donnée sont valides, le pourcentage d’intervalles de confiance qui comprennent la valeur réelle de la population serait approximativement égal au niveau de confiance.
Dans l’exemple illustré à la figure, tous les intervalles de confiance sauf un renferment le paramètre réel de population.
La largeur de l’intervalle de confiance associé à une estimation indique le degré d’incertitude de l’estimation. Si deux estimations sont égales, mais que l’une possède un intervalle de confiance de 95 % qui est plus large que l’autre, l’estimation avec l’intervalle plus large comporte une plus grande incertitude.
Les types d’incertitude reflétés dans les intervalles de confiance pour les estimations du formulaire détaillé diffèrent selon le type de strate. Étant donné que les intervalles de confiance sont fondés sur des estimations de variance, ils reflètent les mêmes types d’incertitude que les estimations de variance sous-jacentes. Dans les unités de collecte (UC) d’envoi par la poste, de listage/livraison et d’envoi par la poste et livraison à la porte, où la fraction de sondage est égale au quart, l’incertitude mesurée est due à l’échantillonnage et à la non-réponse totale. Dans les UC situées dans les communautés des Premières Nations, les établissements métis, les régions inuites et d’autres régions éloignées, où tous les ménages font partie de l’échantillon, l’incertitude mesurée tient compte uniquement de la non-réponse totale.
7.2 Construction d’intervalles de confiance
Les intervalles de confiance sont généralement basés sur les propriétés d’une expression mathématique appelée un pivot. Selon le pivot utilisé et les hypothèses faites sur les propriétés du pivot, différents types d’intervalles de confiance en résulteront. Lors de la construction d’un intervalle de confiance pour un paramètre de population
,
le pivot utilisé fera généralement intervenir l’estimation de thêta, désignée par
,
et l’erreur-type de
.
L’erreur-type d’une estimation est définie comme étant la racine carrée de la variance estimée de l’estimation. L’erreur-type de
est désignée par
.
Le pivot peut également faire intervenir d’autres quantités. La méthode de l’intervalle de Wald, qui est la méthode d’estimation d’intervalles de confiance la plus répandue, est basée sur le pivot suivant :
L’intervalle de Wald suppose que la distribution de ce pivot suit approximativement une distribution normale standard, c’est‑à‑dire une distribution normale avec une moyenne de 0 et un écart-type de 1. La borne inférieure (LB) et la borne supérieure (UB) de l’intervalle de confiance de Wald de 95 % pour le paramètre de population
sont données par :
où
est le 97,5e centile de la distribution normale standard.
Dans de nombreuses situations, l’hypothèse selon laquelle le pivot de Wald est approximativement normal n’est pas respectée. Lorsque les hypothèses qui sous-tendent la construction d’un intervalle de confiance ne sont pas respectées, cela peut donner lieu à une sous-couverture de l’intervalle de confiance. En d’autres mots, si on répétait les procédures d’échantillonnage et d’estimation un très grand nombre de fois et que l’on construisait les intervalles de confiance correspondants pour chaque estimation en utilisant la même méthode, la proportion de ces intervalles de confiance qui contiendraient la valeur réelle de la population pourrait être inférieure au niveau de confiance déclaré.
Pour réduire le risque de sous-couverture, des méthodes plus élaborées que la méthode de Wald ont été utilisées pour produire les intervalles de confiance des estimations du questionnaire détaillé. Ces méthodes offrent une couverture plus proche du taux nominal. Cependant, toutes les méthodes de construction d’intervalles de confiance reposent sur des hypothèses qui ne peuvent être vérifiées explicitement dans des cas d’utilisation particuliers. Lorsqu’ils travaillent avec des intervalles de confiance, les utilisateurs de données doivent garder à l’esprit les cas susceptibles de conduire à ce que les hypothèses sous-jacentes à la construction des intervalles de confiance soient invalides. Les différentes méthodes utilisées pour produire les intervalles de confiance pour les estimations du formulaire détaillé, ainsi que les hypothèses requises, sont décrites en détail dans les sections suivantes.
7.3 Intervalle de confiance de Student
L’intervalle de confiance de Student est utilisé pour toutes les statistiques, sauf les proportions et les comptes. Étant donné que les proportions et les comptes constituent la plupart des estimations diffusées pour le questionnaire détaillé, cette méthode n’est utilisée que pour une minorité des intervalles de confiance diffusés.
L’intervalle de confiance de Student est fondé sur le même pivot que l’intervalle de Wald. Cependant, plutôt que de supposer que la distribution de ce pivot peut être approximée par une distribution normale, la distribution d’approximation est présumée suivre une distribution t de Student. Cette distribution est connue pour être une distribution d’approximation plus appropriée pour le pivot dans les cas où la taille de l’échantillon est petite. La distribution t de Student est définie par un seul paramètre appelé « degrés de liberté ». Le nombre de degrés de liberté de la distribution t de Student est influencé par le plan d’échantillonnage, le nombre d’unités échantillonnées et la méthode d’estimation de la variance. Le nombre de degrés de liberté a une incidence sur la largeur de l’intervalle de confiance. Dans le cas du Recensement de 2021, les degrés de liberté ont été approximés par le nombre de répliques utilisées pour l’estimation de la variance (voir la section 6.2) et désigné par
.
La borne inférieure et la borne supérieure de l’intervalle de confiance de Student de 95 % pour un paramètre de population d’intérêt
sont données par :
où
-
est l’estimation de
;
-
est le 97,5e centile de la distribution t de Student à
degrés de liberté;
-
est l’erreur-type de
.
7.3.1 Propriétés de l’intervalle de confiance de Student
La distribution t de Student est presque identique à une distribution normale standard lorsque le nombre de degrés de liberté est très élevé. Lorsque le nombre de degrés de liberté est petit, la distribution t de Student est plus large que la distribution normale standard. Par conséquent, l’intervalle de confiance de Student est plus large que l’intervalle de Wald pour la même estimation. Les intervalles de Wald font souvent l’objet d’une sous-couverture lorsque la taille de l’échantillon est petite. Bien que le questionnaire détaillé du recensement ait une grande taille d’échantillon pour l’ensemble du pays, la taille de l’échantillon dans les petites régions géographiques ou les petits domaines d’intérêt peut être petite. Dans ces cas, l’intervalle de confiance de Student aura généralement une meilleure couverture que l’intervalle de Wald.
En pratique, l’intervalle de confiance de Student peut tout de même faire l’objet d’une sous-couverture dans les cas où les tailles d’échantillon sont très petites. Cela est dû aux insuffisances des hypothèses lorsque la taille de l’échantillon est très petite. Par exemple, la distribution du pivot peut ne pas être approximée adéquatement par une distribution t de Student, ou l’approximation du nombre de degrés de liberté par le nombre de répliques peut surestimer considérablement les degrés de liberté réels de la distribution. La décomposition de ces hypothèses lorsque la taille de l’échantillon est très petite entraînera généralement une sous-couverture des intervalles de confiance de Student.
7.4 Intervalle de confiance de Wilson modifié pour les proportions
Il existe plusieurs méthodes différentes de construction d’intervalles de confiance pour les proportions. Pour le Recensement de 2021, la méthode d’intervalle de confiance de Wilson modifié a été choisie en raison de sa couverture généralement supérieure et des aspects pratiques de sa mise en œuvre. Cette méthode est utilisée pour toutes les statistiques de proportion. La méthode est basée sur l’intervalle de confiance de Wilson pour un plan d’échantillonnage aléatoire simple avec remise (EASAR) (Wilson 1927). Pour le recensement, une version modifiée de cet intervalle de confiance est utilisée afin de tenir compte du plan de sondage complexe (Kott et Carr 1997). De nombreuses études par simulation ont montré que cette méthode donne de meilleurs résultats que les intervalles de confiance de Wald et de Student dans les situations où ces intervalles de confiance produisent une sous-couverture pour les proportions (Neusy et Mantel 2016; Statistique Canada 2023).
Pour les proportions, l’hypothèse selon laquelle le pivot utilisé pour construire l’intervalle de confiance de Student suit une distribution t de Student ne tient pas dans le cas de petites tailles d’échantillon et lorsque la statistique prend des valeurs près de 0 ou de 1. L’intervalle de confiance de Wilson modifié pour une proportion
est plutôt basé sur le pivot suivant :
où
-
est l’estimation de
;
-
est la taille effective de l’échantillon;
-
est l’effet de plan estimé associé à
par rapport à un plan de sondage EASAR;
-
est la taille de l’échantillon dans le champ de l’enquête;
-
est la variance estimée de
.
La taille de l’échantillon dans le champ de l’enquête est définie comme étant le nombre d’unités échantillonnées qui sont dans le champ d’enquête pour la question correspondant à la proportion
,
c’est-à-dire le nombre d’unités échantillonnées auxquelles la question s’applique et qui appartiennent à la population d’intérêt liée à la question. L’expression sous la racine carrée dans le dénominateur du pivot correspond à la variance de l’estimation de la proportion sous un plan de sondage EASAR, mais dont la taille de l’échantillon a été remplacée par la taille effective de l’échantillon. En utilisant la taille effective de l’échantillon dans cette expression, la variance est ajustée pour tenir compte du plan d’échantillonnage complexe du formulaire détaillé du recensement. L’intervalle de confiance de Wilson modifié est basé sur l’hypothèse que ce pivot suit approximativement une distribution t de Student. Comme pour l’intervalle de confiance de Student, pour le Recensement de 2021, le nombre de degrés de liberté de la distribution t de Student est approximé par
,
le nombre de répliques utilisées pour l’estimation de la variance.
La borne inférieure et la borne supérieure de l’intervalle de confiance à 95 % de Wilson modifié pour la proportion
sont données par :
où
est le 97,5e centile de la distribution t de Student à
degrés de liberté et les autres termes sont définis comme ci-dessus.
7.4.1 Propriétés de l’intervalle de confiance de Wilson modifié pour les proportions
En plus d’obtenir une meilleure couverture que les intervalles de confiance de Wald et de Student pour les petites tailles d’échantillons, et lorsque le paramètre de population est près de 0 ou de 1, l’intervalle de confiance de Wilson modifié pour une proportion donnée possède la propriété désirable d’avoir une borne inférieure qui n’est jamais inférieure à 0 et une borne supérieure qui n’est jamais supérieure à 1. Étant donné que les proportions ne peuvent prendre de valeurs en dehors de l’intervalle de 0 à 1, on peut s’attendre à ce que les intervalles de confiance pour les proportions excluent les valeurs négatives et les valeurs supérieures à 1.
Il convient également de noter que, contrairement aux intervalles de Wald et de Student, l’intervalle de confiance de Wilson modifié pour les proportions est asymétrique, ce qui signifie que l’estimation ne se situera pas exactement au centre de l’intervalle. L’asymétrie est faible lorsque la taille d’échantillon effective est grande ou lorsque la proportion estimée est près de 0,5.
Tout comme les intervalles de confiance de Wald et de Student, l’intervalle de confiance de Wilson modifié pour les proportions peut faire l’objet d’une certaine sous-couverture, particulièrement lorsque la taille d’échantillon est très petite, que la valeur de la proportion est près de 0 ou de 1 ou qu’il existe une forte corrélation entre les membres d’un même ménage. Néanmoins, la méthode de Wilson modifié atteint généralement le taux de couverture nominal dans des situations extrêmes comparativement aux méthodes de Wald et de Student. En général, elle maintient une couverture aussi bonne sinon meilleure que es méthodes de Wald et de Student dans ces situations.
7.5 Intervalle de confiance de Wilson modifié pour les comptes
Pour les estimations des comptes du questionnaire détaillé, la méthode de l’intervalle de confiance utilisée est une méthode de Wilson modifiée semblable à la méthode utilisée pour les statistiques de proportion. Pour les comptes, les intervalles de confiance de Wald et Student n’atteignent pas la couverture nominale lorsque la taille de l’échantillon est petite et lorsque la valeur de la variable d’intérêt est nulle pour presque toutes les unités échantillonnées ou lorsque la valeur est de 1 pour presque toutes les unités échantillonnées. Dans ces situations, la distribution du pivot utilisé pour construire les intervalles de confiance de Wald et de Student n’est généralement pas bien approximée par une distribution normale ou une distribution t de Student.
L’intervalle de confiance de Wilson modifié pour les comptes a été élaboré pour le Recensement de 2021 en tant que solution de rechange aux intervalles de confiance de Wald et de Student pour offrir une couverture plus proche du taux nominal. Il a été testé dans un environnement simulé semblable à celui du formulaire détaillé du recensement et s’est avéré en mesure d’atteindre une bonne couverture (Neusy et coll., 2021).
7.5.1 Intervalle de confiance de Wilson modifié pour les comptes : forme théorique
La version de l’intervalle de confiance de Wilson modifié pour les comptes utilisée dans le cadre du Recensement de 2021 est une approximation d’une forme théorique de l’intervalle. La forme théorique peut être dérivée à l’aide d’une méthode comparable à celle qui a été employée pour l’intervalle de confiance de Wilson modifié pour les proportions. Dans le cas de l’intervalle de confiance de Wilson modifié pour les comptes, la formulation est fondée sur la notion de groupe de calage d’intérêt. Un groupe de calage est un ensemble d’unités pour lesquelles les poids de sondage sont calés pour respecter les totaux de contrôle (pour le questionnaire détaillé du recensement, les groupes de calage correspondent aux ADA et aux SADA), et un groupe de calage d’intérêt pour un compte
correspond à un groupe de calage qui pourrait potentiellement renfermer des unités qui présentent la caractéristique d’intérêt pour
.
L’intervalle de confiance de Wilson modifié pour un compte
est basé sur le pivot suivant :
où
-
est l’estimation de
;
-
est la taille totale de la population des groupes de calage d’intérêt;
-
est la taille totale d’échantillon effective dans les groupes de calage d’intérêt;
-
est la taille totale d’échantillon dans les groupes de calage d’intérêt;
-
est l’effet de plan estimé associé à
par rapport à un plan de sondage d’EASAR, avec les tailles de population et d’échantillon déterminées en fonction des groupes de calage d’intérêt;
-
est la variance estimée de
.
Les tailles de population et d’échantillon sont définies par rapport aux groupes de calage d’intérêt, car cela donne un intervalle de confiance avec de bonnes propriétés. Plus précisément, les simulations montrent que l’intervalle de confiance résultant possède de meilleures propriétés de couverture que les autres façons de définir les tailles de population et d’échantillon (Neusy et coll., 2021).
Tout comme l’intervalle de confiance de Wilson modifié pour les proportions, l’intervalle de confiance de Wilson modifié pour les comptes est basé sur l’hypothèse que le pivot suit approximativement une distribution t de Student. Comme tous les intervalles de confiance du Recensement de 2021, le nombre de degrés de liberté de la distribution t de Student est approximé par
,
le nombre de répliques utilisées pour l’estimation de la variance.
À partir du pivot ci-dessus, la version théorique de l’intervalle de confiance de Wilson modifié de 95 % pour un compte
peut être établie. Cette version de l’intervalle a les bornes inférieure et supérieure suivantes :
où les termes sont définis comme ci-dessus. Dans cette version de l’intervalle, la similitude avec l’intervalle de confiance de Wilson modifié pour les proportions est apparente.
7.5.2 Intervalle de confiance de Wilson modifié pour les comptes : forme approximative
La forme approximative de l’intervalle de confiance de Wilson modifié pour les comptes qui a été mis en œuvre pour le Recensement de 2021 est basée sur l’intervalle théorique ci-dessus. Une approximation a été utilisée en raison des limites du système de tabulation du recensement.
Dans la forme approximative, la borne inférieure et la borne supérieure de l’intervalle de confiance de Wilson de 95 % modifié pour un compte
sont données par :
où
-
est l’estimation de
;
-
est le 97,5e centile de la distribution t de Student à
degrés de liberté;
-
est la variance estimée de
.
7.5.3 Hypothèses pour l’approximation de l’intervalle de confiance de Wilson modifié pour les comptes
Il a été démontré empiriquement que la méthode d’approximation mise en œuvre pour le recensement convient aux plans d’échantillonnage semblables à celui du questionnaire détaillé (Neusy et coll., 2021). L’approximation est basée sur les hypothèses suivantes :
- La taille totale de l’échantillon dans les groupes de calage d’intérêt
est suffisamment grande pour que
soit proche de 0.
- Le nombre estimé
est beaucoup plus petit que la taille totale de la population des groupes de calage d’intérêt
.
La première hypothèse est généralement valide pour le questionnaire détaillé du recensement, car les groupes de calage d’intérêt correspondent aux SADA ou aux ADA, qui ont toujours une très grande taille d’échantillon. La deuxième hypothèse peut ne pas être respectée, mais uniquement pour des caractéristiques communes et pour de très grands domaines d’intérêt, tels que les SADA. Dans cette situation, la version approximative de l’intervalle de confiance de Wilson modifié est presque identique à l’intervalle de confiance de Student, et la performance des deux méthodes est assez bonne dans le cas de grands domaines d’estimation. Par conséquent, le non-respect de la deuxième hypothèse ne pose pas de problème particulier pour le questionnaire détaillé du recensement.
7.5.4 Propriétés de l’intervalle de confiance de Wilson modifié pour les comptes
L’intervalle de confiance de Wilson modifié pour les comptes a un avantage par rapport aux intervalles de confiance de Wald et de Student, soit d’avoir une borne inférieure qui n’est jamais inférieure à 0. Cette propriété, ainsi que les autres propriétés décrites dans cette section, s’applique à la fois à la version théorique et à la version approximative de l’intervalle de confiance. Étant donné que la valeur des comptes ne peut pas être négative, il convient que l’intervalle de confiance ne contienne pas de valeurs négatives. Comme pour l’intervalle de confiance de Wilson modifié pour les proportions, l’intervalle de confiance de Wilson modifié pour les comptes est asymétrique. Cette asymétrie sera faible lorsque la variance estimée d’un compte est petite par rapport au compte estimé lui-même.
Tout comme les intervalles de confiance de Wald et de Student, l’intervalle de confiance de Wilson modifié pour les comptes peut faire l’objet d’une certaine sous-couverture, particulièrement lorsque la taille d’échantillon est très petite, que la valeur du compte est près de 0 ou près de la taille de la population du domaine d’intérêt ou qu’il existe une forte corrélation entre les membres d’un même ménage. Néanmoins, la méthode de Wilson modifié atteint généralement le taux de couverture nominal dans des situations extrêmes comparativement aux méthodes de Wald et de Student. En général, elle maintient une couverture aussi bonne sinon meilleure que les méthodes de Wald et de Student dans ces situations.
